TRIG FUNCTIONS QUESTIONS AND ANSWERS GRADE 12 trigonometric function, in mathematics, one of six functions (sine [sin], cosine [cos], tangent [tan], cotangent [cot], secant [sec], and cosecant [csc]) that represent ratios of sides of right triangles. These six trigonometric functions in relation to a right triangle are displayed in the figure
Activity 1
Use the graph y = sin x above to answer these questions:
- What are the maximum and minimum values of y = sin x? (2)
- Write down the domain and the range of y = sin x. (4)
- Write down the x-intercepts of y = sin x. (2)
- What is the amplitude of the graph of y = sin x? (1)
- What is the period of the graph of y = sin x? (1)
[10]
| Solutions | ||
| y = sinx | ||
| 1 | Maximum Values | 1 , at x = –270° and 90° |
| Minimum Values | –1, at x = –90° and 270° (2) | |
| 2 | Domain | x ∈ [− 360°;360°], x ∈ ℝ |
| Range | [–1; 1] y ∈ ℝ (4) | |
| 3 | x-intercepts | –360°, –180°, 0°, 180° and 360° (2) |
| 4 | Amplitude | 1(1) |
| 5 | Period | 360° (1) |
| [10] | ||
Activity 2
- Given f(x) = 2cos x and g(x) = sin (x + 30°)
- Sketch the graphs of f and g on the same set of axes for x ∈ [− 150°; 180°]
Clearly show all intercepts with the axes and the coordinates of turning points. (7)
Use your graph to answer the following questions: - Write down the period of f. (1)
- For which values of x is f(x) = g(x)? (2)
- For which values of x is f(x) > 0? (2)
- For which values of x is g(x) increasing? (2)
- Determine one value of x for which f(x) − g(x) = 1,5. (1)
- If the curve of f is moved down one unit, write down the new equation of f. (2)
- If the curve of g is moved 45° to the left, write down the new equation of g. (2)
- Sketch the graphs of f and g on the same set of axes for x ∈ [− 150°; 180°]
- Sketch below are the graphs of g(x) = asin(x+p) and f(x) = bcosqx for x ∈ [0°; 180°]
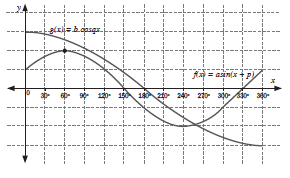
- Determine the numerical values of a, p, b and q. (5)
- If the graph of g(x) is shifted two units down:
- Write down the amplitude of the new graph (1)
- Write down the equation of the new graph (2)
- If the graph of f(x) is shifted 60 to the left, write down two possible equations of the new graph. (2)
[29]
Solutions
|


